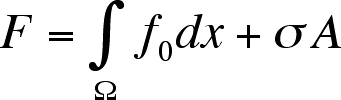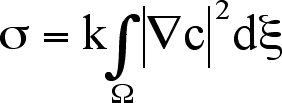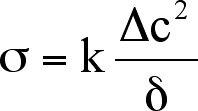The interfacial tension between immiscible fluids is an equilibrium thermodynamic property that results from the differences in intermolecular interactions between the two different types of molecules. When two miscible fluids are brought in contact, a large concentration (and density) gradient can exist, which relaxes through diffusion as the system approaches the uniform, equilibrium state. Because the molecules have different structures, there are necessarily differences in intermolecular interactions, which may lead to transient interfacial phenomena.
For most immiscible systems an infinitely narrow interface, consisting of a discontinuous jump in concentration, was an accurate description. However, for polymer systems and systems near their critical point an infinitely narrow transition zone does not apply. (Nor does it apply to the transition zone between two miscible fluids.) Van der Waals was the first to propose an alternate definition of an immiscible interface [1]. He assumed that the interface consisted of a continuous region, in which there was a transition in concentration from one fluid to the other. Fig. 1 depicts such a transition zone, with increasing concentration from right to left. The interface is then also defined by the width, d, of the transition zone.


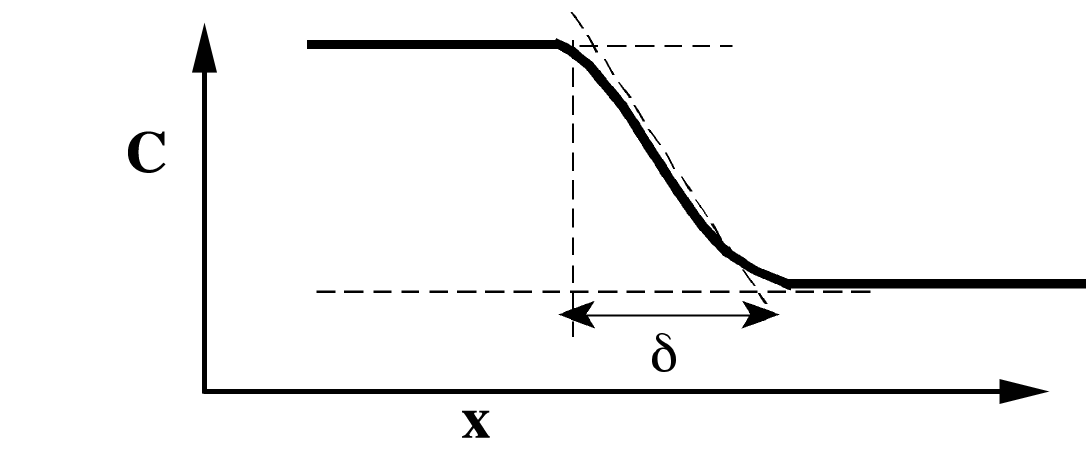
Fig. 1 Schematic of a diffuse interface.

A thermodynamically stable interface can only exist between two immiscible fluids. Nonetheless, we use the term “miscible interface” to designate the transition zone between two miscible fluids, which will necessarily relax with time. Stresses at a miscible interface were first explored by Korteweg [2]. He demonstrated that in the presence of a compositional gradient, stresses would result that would be analogous to stresses in immiscible fluids. Lowengrub and Truskinovsky gave a thorough derivation of the Korteweg stress [3].
Zeldovich published an excellent work in which he showed that an interfacial tension should exist between miscible fluids brought into contact [4]. Davis proposed that when two miscible fluids are placed in contact they will immediately begin to mix diffusively across the concentration front, and the composition inhomogeneities can give rise to pressure anisotropies and to a tension between the fluids [5]. Rousar and Nauman, following the work of Rowlinson and Widom [6], proposed that an interfacial tension can be found without assuming that the system is at equilibrium [7].
There have been several reports of phenomena in which the authors invoke an interfacial tension with miscible systems [8-12]. Joseph and Renardy provided a superb review of the topic up to 1992 [13].
Pojman et al. provided definitive evidence for an effective interfacial tension (EIT) in the isobutyric acid – water system [14]. They showed that after a temperature jump above the Upper Critical Solution Temperature, a drop of the IBA-rich phase persisted in a spinning drop tensiometer. The interfacial tension was on the order of 0.001 mN/m. Drops contracted when the rotation rate was slowly decreased but drops broke up via the Rayleigh-Tomotika instability when the rotation rate was rapidly decreased. Lombardo et al. studied 1-butanol in water in which the drop volume of 1-butanol was so small that the concentration was below the solubility limit [15]. They also were able to measure an EIT.
The Korteweg term for miscible systems far from equilibrium can be compared to Cahn and Hilliard’s treatment of immiscible fluids at equilibrium. Using the Landau-Ginzburg free energy functional they were able to show that the free energy of a non-uniform immiscible system includes a term proportional to the square of the concentration gradient [16]. This is precisely the same situation Korteweg considered for miscible systems far from equilibrium.

For a system far from equilibrium the free energy functional can be written as

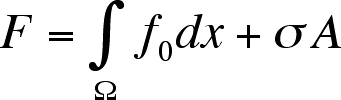
where f0 is the free energy of the uniform system and

.
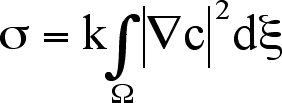
is the effective interfacial tension (EIT), and A the area of the interface. This function can be reduced if we assume a linear concentration gradient. The resulting equation for the EIT is

.

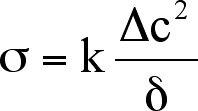
Here the EIT is written in terms of the Korteweg term, , henceforth referred to as the square gradient parameter (with units of Newtons, N), the change in composition , expressed as a mole fraction, and the width of the transition zone, .

Chen and Meiburg have performed numerical simulations of miscible displacement that included Korteweg stress [17-20]. Volpert et al. simulated convection caused by curvature in drops in a miscible system [21]. Bessonov et al. simulated Marangoni-like convection for a miscible monomer-polymer system caused by concentration and temperature gradients parallel to the transition zone between the fluids [22-24].
The problem of testing these predictions on Earth is that buoyancy-driven convection dominates the system. If a stream of honey is injected into water, it will sink because honey is denser than water. If a blob of water is injected into honey, the water will float. Joseph and Renardy attempt to create an isopycnic system with glycerol and sugar water [13]. However, diffusion always upset the delicate balance between the densities of the fluids. Performing experiments in weightlessness is an excellent approach to attempt to observe behavior that can be attributed to Korteweg stress. If no behavior beyond diffusion is observed, it will allow the estimate of an upper limit on the value of the square gradient parameter. We have previously performed experiments with glycerol and water on parabolic flights [21]. No convection was observed but because of the short duration and poor quality of the weightlessness, no conclusions could be drawn.

A major problem for predicting the potential importance to Korteweg stresses in miscible fluids is estimating the value of the square gradient parameter for a pair of miscible fluids. By comparing simulations to the results of this investigation, we will be able to put an upper limit on the value of the square gradient parameter for honey and water.

The Experiment -- MFMG

Back to the Main MFMG Page