1. Introduction - A Bit of History

Oscillations of chemical origin have been present as long as life itself. Every living system contains scores, perhaps hundreds, of chemical oscillators. The systematic study of oscillating chemical reactions and of the broader field of nonlinear chemical dynamics is, however, of considerably more recent origin. In this chapter, we present a brief and extremely idiosyncratic overview of some of the history of nonlinear chemical dynamics.

In 1828, Fechner described an electrochemical cell that produced an oscillating current, the first published report of oscillations in a chemical system [Fechner, 1828]. Ostwald observed in 1899 that the rate of chromium dissolution in acid periodically increased and decreased [Ostwald, 1899]. Because both systems were inhomogeneous, it was believed then, and through much of our own century, that homogeneous oscillating reactions were impossible. Degn wrote in 1972: "It is hard to think of any other question which already occupied chemists in the nineteenth century and still has not received a satisfactory answer [Degn, 1972]." In that same year, though, answers were coming. How it took so long for the nature of oscillating chemical reactions to be understood and how that understanding eventually came about will be the major focus of this chapter.

Although oscillatory behavior can be seen in many chemical systems, we shall concentrate primarily on homogeneous, isothermal reactions in aqueous solution. In later chapters we shall broaden our horizons a bit. While the study of oscillating reactions did not become well-established until the mid 1970's, theoretical discussions go back to at least 1910. We consider here some of the early theoretical and experimental work that led up to the ideas of Prigogine on nonequilibrium thermodynamics and to the experimental and theoretical work of Belousov, Zhabotinsky, Field, Körös and Noyes, who did much to persuade chemists that chemical oscillations, traveling fronts and other phenomena that now comprise the repertoire of nonlinear chemical dynamics were deserving of serious study.

1.1 Lotka-Volterra model

Alfred Lotka was one of the more interesting characters in the history of science. He wrote a handful of theoretical papers on chemical oscillation during the early decades of this century and authored a monograph on theoretical biology that is filled with insights that still seem fresh today [Lotka, 1925]. He then left science and spent the majority of his working life in the employ of an insurance company. In 1910, Lotka [Lotka, 1910] showed that a set of consecutive reactions can give rise to damped oscillations on the way to equilibrium. He continued his search for oscillatory behavior arising from mass action kinetics in a second paper published a decade later [Lotka, 1920a]. This latter model, though it does not apply to any real chemical system, has provided considerable inspiration to ecologists. Vito Volterra used ideas similar to Lotka's to investigate a wide range of ecological problems, including the effects of migration and of several species simultaneously interacting [D'Ancona, 1954]. The best known model of this type is today called the Lotka-Volterra model and is often used to characterize predator-prey interactions [Lotka, 1920a;Lotka, 1920b;Volterra, 1926].

The model consists of three irreversible steps. X is the population of rabbits, which reproduce autocatalytically. A is the amount of grass, which we assume to be constant, or at least in great excess compared to its consumption by the rabbits. Y is the population of lynxes (bobcats), and P represents dead lynxes.

A + X --> 2X (1.1)

X + Y --> 2Y (1.2)

Y --> P (1.3)

As indicated, each step is irreversible: rabbits will never turn back into grass, nor dead lynxes into live ones. We can write down a system of differential equations to describe the behavior of the predator and prey species.

dx/dt = kxax - kyxy (1.4)

dy/dt = kyxy - kdy (1.5)

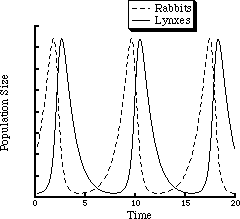
where kx is a rate constant reflecting how fast rabbits reproduce, ky specifies how fast lynxes reproduce given a number, x, of rabbits to eat, and kd indicates the mortality rate of lynxes. For any set of these constants, the numbers of rabbits and lynxes will oscillate with a period that depends upon kx, ky, kd and a. The "net reaction," which proceeds monotonically, is the conversion of grass, which is assumed to grow as fast as it is consumed, to dead lynxes. Figure 1.1 shows the oscillations in the rabbit and lynx populations.

Figure 1.1 Numerical solution of the Lotka-Volterra model with a = kx = ky = kd = 1.

A key feature of this system, and of most chemical systems that exhibit oscillations, is autocatalysis, which means that the rate of growth of a species, whether animal or chemical, increases with the population or concentration of that species. Even autocatalytic systems can reach a steady state, in which the net rate of increase of all relevant species is zero, e.g., the rate of reproduction of rabbits is exactly balanced by that species' consumption by lynxes, and lynxes die at the same rate that baby lynxes are born. Mathematically, we find such a state by setting all the time derivatives equal to zero and solving the resulting algebraic equations for the populations. As we shall see later, a steady state is not necessarily stable; that is, the small perturbations or fluctuations that always exist in a real system may grow, causing the system to evolve away from the steady state.

The oscillations in the two populations result from the difference in phases between rabbit reproduction and lynx reproduction. The rabbits reproduce because grass, A, is in constant supply. The lynx population will also increase, but only after the rabbit population has grown. Once the lynx population gets too high, since the grass supply is limited, rabbits will be eaten more rapidly than new rabbits are born, and their population will begin to decrease, which in turn will lead to a decrease in the lynx population. The rabbit population can then begin to rise again. Thus there will be a time lag between changes in the two populations.

1.1.1 Experimental Evidence

Figure 1.2 shows the number of lynx furs turned in to the Hudson Bay Company from 1820 to 1920. Distinct oscillations are seen with a period of about nine years. No data were available on the rabbit population, so we can not be certain that the oscillations are due to a predator-prey interaction. However, controlled experiments have been performed in the laboratory with paramecia (paramecium aurelia) that eat the yeast saccharomyces exiguns. (Figure 1.3). Notice how the predator population lags behind the population changes in the prey.

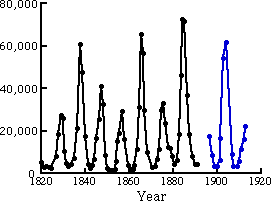
Figure 1.2 Lynx furs return from the Northern Department of the Hudson Bay Co. Adapted from [D'Ancona, 1954].

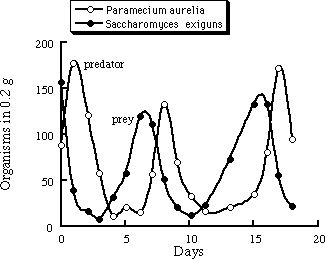
Figure 1.3 Oscillations in the populations of paramecia and yeast. Adapted from [D'Ancona, 1954].

1.2 Bray reaction

The first homogeneous isothermal chemical oscillator to be described was the reaction of iodate, iodine and hydrogen peroxide, studied by William C. Bray at the University of California, Berkeley, and later by Bray's student Herman Liebhafsky [Bray, 1921;Bray and Liebhafsky, 1931]. Hydrogen peroxide decomposes to oxygen and water. The rate of evolution of oxygen and the I2 concentration were found to vary nearly periodically (Figure 1.4). Nonetheless, for the next fifty years, chemists would write that the reaction was not really homogeneous and that the oscillations were an artifact of dust or bubbles. In Bray's 1921 publication, he explicitly addressed these possible objections by using carefully filtered and stirred solutions at room temperature. The rate of reaction was so slow that oxygen diffused out before bubbles could form.

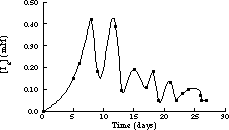
Figure 1.4 Oscillations in the iodine concentration in the Bray reaction at 25 °C. Adapted from [Bray, 1921].

Noyes and coworkers [Sharma and Noyes, 1975] revived the work of Bray and Liebhafsky in the 1970's and, through careful experiments and mathematical modeling, building on the theoretical groundwork that had been laid by studies of nonequilibrium thermodynamics, succeeded in convincing the chemical community that the Bray reaction represented a genuine chemical oscillator.

1.3 The Belousov-Zhabotinsky reaction

The beginning of modern nonlinear chemical dynamics can be traced to Boris Pavlovich Belousov (1893-1970), who was looking for an inorganic analog of the Krebs cycle, a key metabolic process in which citric acid is an intermediate. In 1950 he began his studies while head of the Laboratory of Biophysics in the USSR Ministry of Health. (Before the 1917 revolution, Belousov had studied chemistry in Zurich.) He investigated a solution of bromate, citric acid and ceric ions (Ce4+). He expected to see the monotonic conversion of yellow Ce+4 into colorless Ce+3. Instead, the solution repeatedly cleared and then became yellow again! He studied the system carefully, including the effects of temperature and initial concentrations. Belousov also noted that, unstirred in a graduated cylinder, the solution exhibited traveling waves of yellow. He submitted a manuscript in 1951, but it was rejected. The editor of one of the unsympathetic journals informed him that his "supposed discovered discovery" was impossible![Winfree, 1984] The paper could only be published if he furnished additional evidence; a simple recipe and photographs of the different phases of oscillation were deemed to be insufficient. He labored six more years and submitted a revised manuscript to another journal, but that editor insisted that the paper be shortened to a letter before further consideration. Belousov decided to give up on publishing his work, but he kept his manuscript, which circulated among colleagues in Moscow. His only publication on this reaction appears in the unrefereed abstracts of a conference on radiation biology [Belousov, 1958]. A manuscript that Belousov wrote in 1951 describing his work was posthumously published in Russian in 1981 [Belousov, 1981] and in English translation in 1985 [Belousov, 1985].

In 1961, Anatol Zhabotinsky, a graduate student in biophysics at Moscow State University, began looking at the same system at the suggestion of his professor, S. E. Schnoll. Although Zhabotinsky did not have Belousov's 1958 paper, he did have access to the original recipe: 0.2 g KBrO3, 0.16 g Ce(SO4)2, 2 g citric acid, 2 mL H2SO4 (1:3) and enough water to make a 10 mL solution. He replaced citric acid with malonic acid and obtained a better formulation, which did not produce precipitate. (Information on experiments and demonstrations is presented in the Appendix.)

Zhabotinsky wrote a manuscript that he sent to Belousov for his comments in 1962. Belousov replied by mail, but avoided any direct meeting, and the two never met face to face. At least ten papers on the Belousov-Zhabotinsky (BZ) reaction were published in Russian before the first one in English [Degn, 1967a;Degn, 1967b]. A conference was held in Prague in 1968 on Biological and Biochemical Oscillators, and Zhabotinsky presented some of his results. This meeting motivated many in the Eastern Bloc to study the BZ reaction, and the publication of the proceedings in English [Chance, et al., 1973] brought the BZ reaction to the attention of several Western chemists as well.

In several of his experiments, Belousov used the redox indicator ferroin to heighten the color change during oscillations. Ferroin is red in reduced solution and blue in oxidized form, providing a more easily visible variation than the pale yellow to colorless change of the ceric-cerous system. Zaikin and Zhabotinsky found that ferroin alone could catalyze the BZ reaction without cerium [Zaikin and Zhabotinskii, 1970]. This advance allowed them to study unstirred solutions in thin layers, in which they discovered propagating chemical waves. Now a homogeneous system was shown to exhibit not only temporal but also spatial self-organization.

In 1980 the Lenin Prize was awarded to Belousov, Zhabotinsky, V. I. Krinsky, G. R. Ivanitsky and A. Zaikin for their work on the BZ reaction. Belousov had died in 1970.

Before, and even during, the development of the BZ reaction, a number of papers were being written in the West on why true homogeneous oscillating reactions were impossible. Some claimed that the Bray reaction was not a homogeneous reaction but instead that the oscillations resulted from the presence of small particles[Rice and Reiff, 1927]. Many believed that the oscillations were an artifact of heterogeneous phenomena like bubble formation [Peard and Cullis, 1951;Shaw and Pritchard, 1968]. Others argued that such spontaneous temporal self-organization (periodic changes in concentration of putative reactants and products) violated the Second Law of Thermodynamics [Swartz, 1969] and references in[Degn, 1972;Winfree, 1984]. To understand why such objections were so influential and why they do not, in fact, preclude chemical oscillation, we need to digress into a brief discussion on thermodynamics.

1.4 The Second Law

Many of those who found themselves unable to accept chemical oscillation as a reality based their refusal on the Second Law of Thermodynamics. The power of the Second Law lies in its ability to predict the direction of spontaneous change from the deceptively simple condition that

Delta Stotal > 0 (1.6)

where Delta Stotal is the total entropy change of an isolated system or of the universe for the change of state of interest. It is the Second Law that forbids those seemingly plausible perpetual motion machines foisted on patent offices by loony inventors or on unsuspecting students by fiendish teachers of physical chemistry.

In chemical reactions it is difficult to keep track of the entropy of the universe. If the reaction is performed under the commonly encountered conditions of constant temperature and pressure, the condition (1.6) becomes equivalent to the requirement that the change in the Gibbs free energy, G, be negative [Atkins, 1995]. The essential result is that there exists a function of state, i.e., a function like the entropy or the free energy, that depends only upon the current condition (temperature, pressure, volume, concentrations) of the system and not on its past history, and that changes monotonically in any spontaneous process, bringing the system ever closer to its final equilibrium state. Those who objected to the notion of oscillating reactions understandably, but mistakenly, considered an oscillating reaction to be analogous to a pendulum, which passes through its equilibrium point during each cycle of oscillation. They thus concluded that an oscillating reaction would require the free energy of the system to oscillate as the reactants were converted to products and then back to reactants., thus contradicting the Second Law. Figure 1.5 shows permissible and invalid temporal evolutions of free energy* .

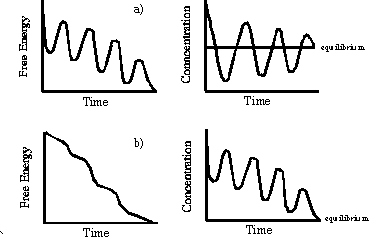
Figure 1.5. Two types of conceivable oscillations in closed systems. a) Oscillations around equilibrium. This is not consistent with the Second Law, because the free energy must monotonically decrease to the equilibrium value. b) Oscillations on the way to equilibrium, consistent with the Second Law.

As the figure indicates, a chemical oscillator is really quite different from a pendulum. When a chemical reaction oscillates, it never passes through its equilibrium point. Instead, chemical oscillation is a far-from-equilibrium phenomenon, governed by the laws of non-equilibrium thermodynamics [de Groot and Mazur, 1984]. Beginning in the 1930's, Lars Onsager, Ilya Prigogine and others realized that thermodynamic ideas could be applied to systems far from equilibrium, but that a new theory was required. Prigogine and his coworkers in Brussels focused on chemical systems, pointing out that a system could organize (decrease its entropy), so long as the net entropy change in the universe was positive[Nicolis and Prigogine, 1977;Nicolis and Prigogine, 1989;Prigogine, 1980]. Thus, for example, the concentrations of the intermediates in a reaction can increase and decrease with time while the free energy monotonically decreases as a result of the continuing conversion of high free energy reactants into low free energy products. Any decrease in entropy caused by the periodic concentration changes is more than compensated by an entropy increase from the other processes (Figure 1.6).

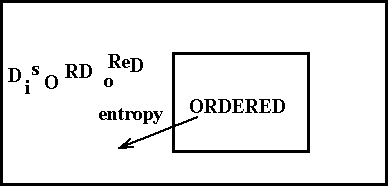
Figure 1.6 Schematic diagram showing how an open system can become ordered but increase the disorder of the surroundings. The overall entropy change of the universe is positive.

Prigogine pointed out in 1955 that open systems, i.e., systems open to exchange of matter and/or energy with their surroundings, kept far from equilibrium could exhibit spontaneous self-organization by dissipating energy to the surroundings to compensate for the entropy decrease in the system [Prigogine, 1955]. He called the temporal or spatial structures that can arise in such a fashion dissipative structures. A closed system must reach equilibrium and so can exhibit only transitory oscillations as it approaches equilibrium. Sustained oscillations require an open system with a constant influx of new reagents and the removal of waste products.

Oscillating reactions no more violate the laws of nature than do living organisms. In our body, the spontaneous formation of proteins occurs even though the DG of peptide bond formation is positive. Protein synthesis occurs because it is coupled to other reactions whose DG is negative, yielding a net decrease in free energy [Lehninger, 1993]. What oscillates in the BZ reaction in a beaker are not the concentrations of reactants (bromate and malonic acid) and products (carbon dioxide and bromomalonic acid), but the concentrations of intermediates such as bromide and bromous acid. The free energy of the reaction is always decreasing as high free energy reactants are continuously converted to low free energy products.

1.5 Nonlinear Oscillations

To understand the role of a system's being far from equilibrium, consider a bottle of beer. If it is gently tipped on its side, the beer will pour out smoothly. However, if you tip the bottle over rapidly, then the beer will gush out in pulsations. A reaction near equilibrium is like the bottle slightly tipped -- it will react smoothly and monotonically. A reaction far from equilibrium can undergo oscillations on the way to equilibrium. To complete our analogy, a beer bottle operating as an open system would have a pump that continuously flows in beer; the pulsating flow could continue indefinitely, much to the delight of the participants in the experiment.

1.6 The Brusselator

Despite the fact that it generates sustained oscillatory behavior from simple "chemical reactions" with mass action kinetics, the Lotka-Volterra model is not an appropriate description of any actual chemical, as opposed to ecological, system. Its fatal flaw is that, in a sense, it is too successful in generating oscillatory behavior. It is possible to prove that the model has an oscillatory solution for any values of the rate constants and "food supply" a and initial values of x and y in eqs. (1.1)-(1.3) and that the amplitude and period of the oscillations obtained depend upon all of these quantities; there is an infinite array of oscillatory solutions. If the system is perturbed, say by adding a bit more a or x or y, it continues to oscillate, but now with a new period and amplitude until it is perturbed again. In the presence of any significant amount of noise, the behavior would hardly be recognizable as periodic, since it would constantly be jumping from one oscillatory behavior to another. Real chemical systems do not behave this way. They oscillate only within a finite range of parameters, and they have a single mode (amplitude and frequency) of oscillation, to which they return if the system is perturbed. Is it possible to construct a reasonable model that has these features? The first chemically "respectable" model was proposed by Prigogine and Lefever in 1968 [Prigogine and Lefever, 1968] and dubbed the "Brusselator" by Tyson in 1973 [Tyson, 1973].

A --> X k1 (1.7)

B + X --> Y + D k2 (1.8)

2X + Y --> 3X k3 (1.9)

X --> E k4 (1.10)

By analysis and numerical simulation, Prigogine and Lefever demonstrated that their model shows homogeneous oscillations and propagating waves like those seen in the BZ system. The Brusselator was extremely important because it showed that a chemically reasonable mechanism could exhibit self-organization.

In 1977, Nicolis and Prigogine summarized the work of the Brussels school in a book entitled Self-Organization in Nonequilibrium Systems [Nicolis and Prigogine, 1977]. For his contributions to the study of nonequilibrium systems, Ilya Prigogine was awarded the 1977 Nobel Prize in Chemistry.

1.7 Back to the BZ Reaction

Although chemical engineers had been considering oscillatory behavior in reactors since 1945 [Higgins, 1967], chemists remained skeptical of claims of oscillations. As Degn [Degn, 1972] described the situation in 1972: "Although there now seems to be abundant evidence for the existence of homogeneous oscillating reactions, there are still theoreticians who resist the idea, and also a few experimentalists think that alleged homogeneous oscillations are caused by dust particles, although nobody has explained how." Despite the existence of the abstract Brusselator model, what was missing was a detailed chemical mechanism for an oscillating reaction to convince chemists that oscillating reactions were a legitimate area of study and not some form of a perpetual motion device.

A chemist wants to understand chemical reactions on the molecular level, and a mechanism is a map of those processes. A mechanism is a series of elementary reactions that involve actual molecular collisions that lead to transformation. To write that 2H2 + O2 Æ 2H2O is not to assert that two molecules of hydrogen collide with one molecule of oxygen and somehow rearrange themselves to fly apart into two molecules of water. This is only the net reaction, which shows the necessary stoichiometry. For a chemist to truly understand the reaction of hydrogen and oxygen, he or she needs to know all the individual steps that lead to the overall reaction. This is an extremely difficult task for all but the simplest of reactions.

Zhabotinsky and his coworkers had made significant progress in understanding the mechanism of the BZ reaction, but their work was largely unknown in the West. Few scientists outside the Eastern bloc could read Russian. Even though many Soviet journals were translated into English, a Cold War mentality, and perhaps a touch of arrogance, prevented most Western scientists from keeping up with that literature. Another more pernicious impediment to scientific exchange was the prohibition on travel. Except in rare cases, Soviet scientists could not attend Western conferences, and few Western scientists were permitted into the Soviet Union. With our faxes and electronic mail, it is difficult to imagine today how isolated the Soviet scientists were.

The first publications in English to recognize the work of Belousov and Zhabotinsky were by the Danish scientist Hans Degn [Degn, 1967a;Degn, 1967b]. He measured the cerium (IV) concentration, platinum electrode potential (responding to the ratio Ce(IV)/Ce(III)), and the evolution of carbon dioxide in the BZ reaction, but he was unable to propose a complete mechanism for the system. The Prague conference in 1968 afforded an opportunity for Zhabotinsky and some of the other Russian scientists to present their work and to meet some of the more intrepid westerners.

1.7 The BZ Reaction Comes to North America

The work that led to the "legitimizing" of the study of oscillating reactions is a fascinating story of serendipity and hard work. In 1969, Richard Field, a recent graduate of the University of Rhode Island began a postdoctoral fellowship with the well known kineticist Richard Noyes at the University of Oregon in Eugene. Robert Mazo, a theorist in the same department, had just returned from a sabbatical year in Brussels with the Prigogine group. In Brussels, Mazo had seen a demonstration of the BZ reaction and of the banding that occurs when the reaction is run in an unstirred graduated cylinder [Busse, 1969]. Mazo presented a seminar in the Oregon chemistry department and demonstrated the banding. After his talk, Noyes wondered if the banding would reappear if the solution were stirred. When he and his coworkers tried the stirred reaction in the lab, they rediscovered the oscillatory behavior!

Field and Noyes were fascinated by the oscillations and set out to determine the mechanism of this remarkable behavior. Endre Körös had recently arrived in Eugene for a sabbatical visit from Eötvös University in Budapest. He had come to study iodine exchange reactions, a specialty of Noyes', but when he saw the BZ reaction, Körös decided to work on it, too. Körös suggested using a bromide-selective electrode to follow the reaction, which proved to be a major boon to understanding the importance of bromide in the reaction. During this period, Kasperek and Bruice carried out a study on the BZ reaction that included some significant additional observations but no mechanism [Kasperek and Bruice, 1971]. This publication spurred the Eugene group, but Bruice discontinued the work, since he was skeptical that the oscillations arose from a purely homogeneous system.

The details of the mechanism that was developed in Eugene are discussed in later chapters. The important fact is that Field, Körös and Noyes were able to explain the qualitative behavior of the BZ reaction using the same principles of chemical kinetics and thermodynamics that govern "ordinary" chemical reactions. They published their mechanism, now know as the FKN mechanism, in a classic paper in 1972 [Field, et al., 1972;Noyes, et al., 1972]. A quantitative numerical simulation of the oscillatory behavior based on the FKN mechanism was published a few years later [Edelson, et al., 1975].

Arthur Winfree, a biologist with an interest in spatial and temporal patterns, had attended the Prague conference and had decided to pursue the study of pattern formation in the BZ reaction. In 1972, the cover of Science magazine featured Winfree's photo of spiral wave patterns in the BZ reaction [Winfree, 1972]. Figure 1.7 shows such patterns. Field and Noyes immediately saw how to understand the development of such patterns with the aid of the FKN mechanism, and they published an explanation the same year[Field and Noyes, 1972].

Figure 1.7 Target patterns and spiral waves in the Belousov-Zhabotinsky reaction observed in a petri dish (courtesy of T. Yamaguchi).

One final step solidified the hold that the BZ reaction and chemical oscillation were taking on the imaginations of chemists in the 1970's. Field and Noyes managed to simplify the FKN mechanism, which, with its twenty or so elementary steps and chemical species, was too large and complicated for numerical work with any but the most powerful computers and software then available, let alone analytical solutions. With penetrating chemical insight, they obtained a model that had only three variable concentrations yet maintained all the essential features of the full BZ reaction. The model was dubbed the "Oregonator" [Field and Noyes, 1974].

Field continued his work as a professor at the University of Montana, Körös returned to Budapest and Noyes continued at Eugene. To this day, Hungarian chemists continue to have a disproportionate impact on the study of oscillations and waves.

1.8 Systematic Design

By the late 1970's many chemists were aware of oscillating reactions and agreed that they were genuine and even interesting. However, only two fundamentally different chemical oscillators, the Bray and the BZ reactions, were known, and both had been discovered by serendipity. Several variants of the BZ reaction had been developed, using other metals in place of cerium to catalyze the reaction, or replacing the malonic acid with a similar organic species, or even a version in which, with an appropriate choice of the organic substrate, no catalyst was required [Orbán and Körös, 1979;Orbán, et al., 1978]. In 1973, two high school chemistry teachers in San Francisco [Briggs and Rauscher, 1973] developed a visually appealing lecture demonstration by combining the malonic acid and the metal ion catalyst of the BZ reaction with the ingredients of the Bray reaction. (A recipe is given in the Appendix.) There were, of course, many biological oscillators known, but as far as chemical oscillators were concerned, the only techniques for finding them, accident and variation on a theme, did not inspire confidence in the ability of chemists to elucidate the nature of these systems. Efforts to specify a nontrivial set of necessary and sufficient conditions for a chemical reaction to oscillate proved fruitless.

In the mid-1970s, two efforts began that were to converge toward a systematic approach to building chemical oscillators. Irving Epstein and Kenneth Kustin at Brandeis University had been working with a few talented undergraduates on some problems related to the BZ reaction [Jacobs and Epstein, 1976;Kaner and Epstein, 1978]. They identified several autocatalytic inorganic reactions which they thought could be turned into new chemical oscillators, and they attempted to obtain support for the project. Their proposal was rejected three times by funding agencies on the grounds that it would never succeed, but they persisted and were eventually funded. Meanwhile, at the Paul Pascal Research Center in Bordeaux, a group of scientists led by Adolphe Pacault had pioneered the use of the continuous flow stirred tank reactor (CSTR), a tool familiar to chemical engineers but essentially unknown to chemists, to provide an open system suited to the study of oscillating reactions [Pacault, et al., 1976]. Two members of the Bordeaux group, Patrick De Kepper and Jacques Boissonade, proposed an abstract model that suggested how oscillations might be obtained in a CSTR by perturbing a bistable chemical system [Boissonade, 1980]. The funding obtained by the Brandeis group made it possible for De Kepper to join them in late 1979. Within a few months the team had developed the first systematically designed oscillating reaction, the arsenite-iodate-chlorite system[De Kepper, et al., 1981a;De Kepper, et al., 1981b]. The technique, which is described in Chapter 4, was quickly refined and then exploited to develop literally dozens of new oscillators over the next decade.

1.9 The Plot Thickens

As the number of chemical oscillators grew in the 1980s, interest turned to more exotic phenomena, several of which are discussed in Part II of this book. Spatial pattern formation, especially the spiral waves seen in the BZ reaction, drew a great deal of interest, both for its own inherent beauty and because of the similar structures seen in a variety of biological systems. The stationary patterns posited by the mathematician Alan Turing in 1952 as a "chemical basis for morphogenesis" [Turing, 1952] were seen for the first time in 1990 [Castets, et al., 1990] in an experimental system derived from one of the systematically designed oscillators of the '80s.

Like their scientific cousins, the physicists, chemists began to explore how coupled and forced oscillators behave. They also probed how their chemical oscillators and patterns were affected by diffusion, convection and external fields. A topic that created great interest among physicists and mathematicians in the 1970s and 1980s is deterministic chaos. A chaotic system is unpredictable, but not random. Deterministic equations describe the system, but the system is so sensitive to its initial conditions that its future behavior is inherently unpredictable beyond some relatively short period of time. Chaos was found in many physical systems, from lasers to water faucets, in the '70s. What then of chemistry? Schmitz and Hudson reported in 1977 that the BZ system behaves chaotically under certain conditions in a flow reactor [Schmitz, et al., 1977]. Further studies in the '80s and '90s have confirmed the existence of chaos in chemical systems and have shed new light on its origins.

1.10 Conclusion

The history we have given here has of necessity left out many important and fascinating details. What we have tried to convey is a sense that nonlinear chemical dynamics has not had an easy path into the hearts and minds of chemists. Skepticism and prejudice delayed for many years the serious study of the phenomena that we shall be discussing. In the end, the combination of persuasive experimental and theoretical work with persistent advocates and visually stimulating phenomena won out. Elements of nonlinear chemical dynamics are now found in "mainstream" textbooks and introductory courses. Research grants are awarded, international conferences are held, junior faculty are hired. In short, the field is now respectable. This book is an effort to make it not only respectable, but accessible and comprehensible.

Many practitioners of nonlinear chemical dynamics have turned toward biological systems, toward geological phenomena and toward materials science. There are likely to be additional exciting applications in the coming decade. Before one can jump into these new areas, it is necessary to acquire the basic tools, which is where we begin the next chapter.