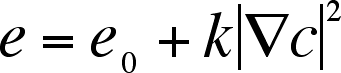
Modeling
We developed a mathematical model for Korteweg stresses in miscible fluids
in which the stress tensor terms are added to the incompressible Navier-Stokes
equation.
We consider mass, energy and momentum conservation. We assume:
a) Thermal and diffusive fluxes are small,
b) The internal energy has the form,
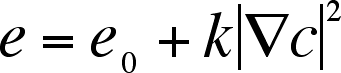
c) Capillary forces are tangential to the composition gradient,
d) The fluids are incompressible and have the same density and viscosity.
We obtain the following model.
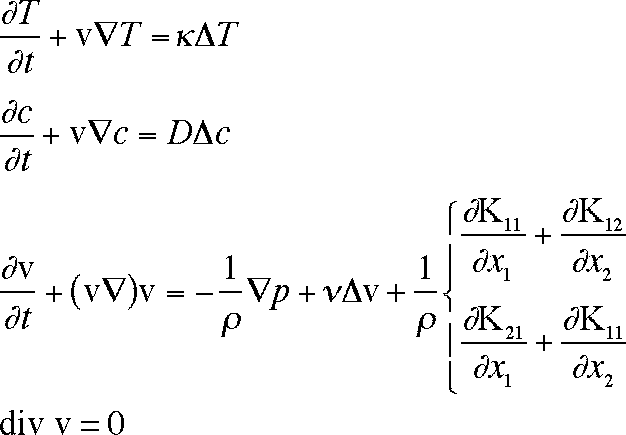
Here T is the temperature, v is the fluid velocity, p is the pressure, n is
the kinematic viscosity, r is the density, and c is the concentration (mole
fraction)
of polymer. Kij are the stress tensor terms, defined by:
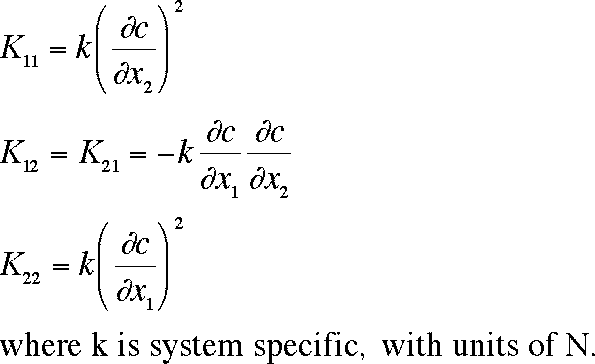
In this analysis we use an adaptive grid formulation. Our method employs conservation
laws (mass, momentum, energy) in integral form. Using integral forms instead
of differentials enables the use of a viscosity that is dependent on concentration
and temperature[32]. In addition we use a “pressure-velocity” instead
of the “stream-function and vorticity” as our basic variables.
For the initial width of the transition zone we used a value of 0.1 mm. The
square gradient parameter, k, was varied until we reached a value at which
no change
in the drop shape was observed.

We obtained two cans of the same type of honey used on the ISS and measured
its viscosity as a function of honey concentration and temperature (Fig. 11)
using
an Anton Paar rheometer. From these data we generated a function where C=1
for pure honey and C = 0 for pure water.
Viscosity (c,T) = (41.5 x 10–5– 1.07 x 10–5T)
e-0.1 C
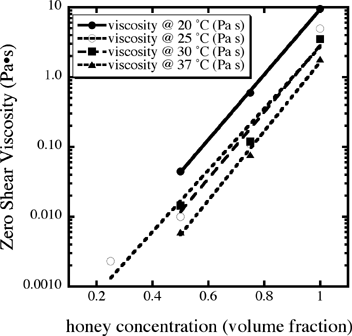
Fig. 11 The zero-shear viscosity as a function of honey fraction in water and
temperature.
Diffusion Coefficient as a function of concentration and temperature
We used the data for fructose, the largest component of honey, from Sano et
al. [33] for the diffusion coefficient as a function of temperature and concentration:
d (c, T) = 7 x 10–10 x 10–a (T) C
, kg/(m s)
a(T) = 4.81 + 8.42/(T+273)
For the simulation of the water injected into honey, we used the image to define the initial conditions. For the stream of honey injected, we only simulated the tip. If the tip does not exhibit any change in shape where the curvature is greatest, then we do not expect the stream to break up.
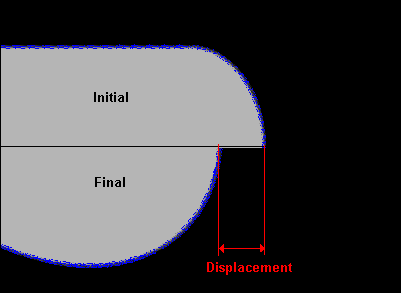
Fig. 12 The initial drop shape for the simulation of a blob of water injected
into honey was taken from the experiments. The displacement would be negative
for this case. d = 0.1 mm
Water into honey
Fig. 12 shows the initial conditions and how the drop can change shape because
of the Korteweg stress. By plotting the displacement of the tip we can determine
if any significant fluid motion should occur for different values of the square
gradient parameter. We note first that the tip initially stretches out and
then the pulls back. Fig. 13 compares two simulations, one with k = 10–10 N
and k = 10–12 N. In both cases the drop makes a small positive
displacement (to the right) and then contracts. Fig. 14 compares both cases
with two more
in which the concentration of honey is decreased. Because the viscosity is
a strong function of concentration, the amount of displacement is much more
pronounced.
In all cases, a very small displacement would be observed after 10 minutes
(600 seconds). We had only requested the observation to proceed for 10 minutes
but
for the last run by John Phillips, we requested an extension to 30 minutes
using the digital camera’s intervalometer. However, bubbles were drawn
into the system, eliminating the value of the run.
Fig. 13. The evolution of a water drop in pure honey for 10–11 N
(Left) and k = 10–12 N (Right)
The height of the domain shown is
0.7 cm, which is half of the total simulation domain.
Fig. 14. Isothermal simulation results for water into honey with initial
conditions shown in Fig. 12. Results for water into pure honey and water
into 80% honey.
Notice the significant effect of a 20% change in honey concentration. 10–11 N
(Left) and k = 10–12 N (Right)
Simulations with a Temperature Gradient
Using the data from Mike Fincke, we calculate the temperature gradient of 5
K over 1.9 cm. We assume it is linear and does not change during the simulations.
Our model is axisymmetric, so during its motion the drop conserves its axisymmetric
shape. However, the temperature gradient can still affect the evolution of
the
drop by creating gradients of the transition zone width. With k = 10–11
N, significant change in the tip shape can be observed (Fig. 15). In Fig. 16,
the tip shape also changes significantly. For k = 10–12 N, some change
in the tip shape might be observable. Since we did not observe such behavior,
we can estimate that k <10–12 N.
Fig. 15 The evolution of the tip of in pure honey injected into water with
an applied temperature gradient, for k = 10–11 N (Left) and
k = 10–12 N (Right).
The temperature gradient was 2 K cm–1.
Discussion
No movement of the drops or streams was observed that could not have been caused
by residual acceleration in the ISS. If our Korteweg-stress model is correct
and if our functions for the viscosity and diffusion coefficient dependences
on temperature and concentration are valid, then we can estimate that the square
gradient parameter for honey and water is less than 10–12 N.
Although these experiments are the first of their kind, they are relatively
crude and filled with uncertainty. The concentrations of water and honey were
only
estimated by the crewmember. The properties of the honey used in the experiments
can only be estimated from the sample we obtained. Finally, we used data for
fructose’s diffusion coefficient but honey is a supersaturated solution
containing many compounds.
Conclusions
For the first time, miscible fluids were studied in microgravity to determine
if they could exhibit transient interfacial phenomena seen with immiscible
fluids. Four experiments were performed with honey and water under isothermal
conditions.
For a stream of honey injected into water, no Rayleigh-Tomotika instability
was observed. A blob of water did not appear to change its shape. Numerical
simulations
indicate that if the Korteweg-stress model is correct then the square gradient
parameter must have a value < 10–12 N.
Two experiments were performed with temperature gradients. For the injection
of diluted honey into water, the stream migrated to the high temperature side
of the syringe but the injection process caused this. Simulations with a temperature-independent
square gradient parameter but a temperature-dependent diffusion coefficient
revealed that the a measurable change in the tip of the drop would have been
observed
if k ≥ 10–12 N.
With all the limitations of a zero-upmass investigation, MFMG was a success
and will hopefully motivate additional microgravity studies with miscible fluids.
ACKNOWLEDGMENTS
Support for this project was provided by NASA’s Microgravity Materials
Science Program (NAG8-1466). We thank the MFMG team for their hard work and
perseverance: Melanie Bodiford, Larry Cotton, Glen Funkhouser, Lucinda Murphy,
Julia Ogle,
Frank Parris, John Yates and Ron Young. We also are deeply indebted to Dr.
Michael Foale, Mike Fincke, Leroy Chiao and Dr. John Phillips for their skill
and hard
work. We also thank Joshua Otaigbe and Kevin Urman for measurement of the
viscosity and thank Anton Paar Physica for the donation of the rheometer.